Drucker-Prager
Das Drucker-Prager-Materialmodell ist das einfachste Materialmodell, das zur Abbildung eines nichtlinearen Bodenverhaltens eingesetzt werden kann. Im Gegensatz zum Mohr-Coulomb-Modell ist die Fließfläche beim Drucker-Prager-Modell glatt und erscheint im Hauptspannungsraum als zylindrischer Kegel.Wie in der untenstehenden Abbildung zu erkennen ist, hängt die Fließfläche – ähnlich wie beim Mohr-Coulomb-Modell – vom mittleren effektiven Spannungszustand σmeff ab. Die in GEO5 FEM implementierte Version des Modells basiert auf der Annahme einer triaxialen Extension.Das bedeutet, dass die Projektion der Drucker-Prager-Fließfläche fDP in eine deviatorische Ebene durch die inneren Ecken des Mohr-Coulomb-Sechsecks verläuft – bei einem Lode-Winkel von, θ = - 30°
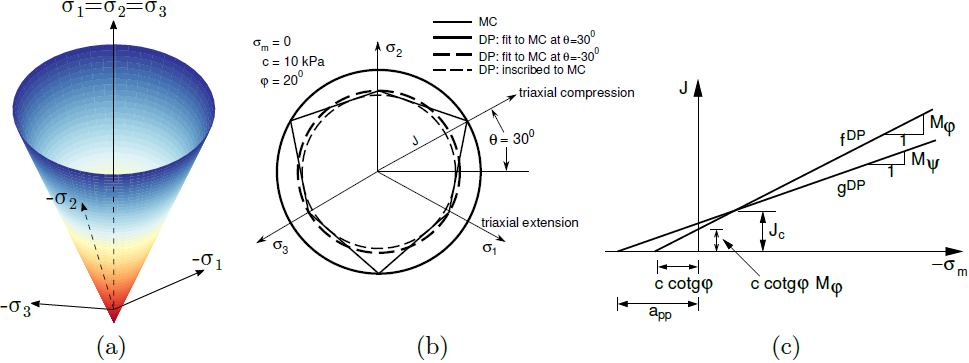 a) Fließfläche im Hauptspannungsraum, b) Projektion in die deviatorische und c) meridionale Ebene
a) Fließfläche im Hauptspannungsraum, b) Projektion in die deviatorische und c) meridionale Ebene
Das Drucker-Prager-Modell ermöglicht die Berücksichtigung der Dilatanz des Materials (d. h. der positiven volumetrischen plastischen Dehnungen während des plastischen Scherens) durch Einführung des Dilatanzwinkels ψ. Die Entwicklung plastischer Dehnungen wird im Allgemeinen durch das plastische Potenzial gDPgesteuert. Während die Steigung der Fließfläche in der Meridionalebene durch den inneren Reibungswinkel Mφ = Mφ(φ)bestimmt wird, hängt die Steigung der Plastischen-Potenzialfläche vom Dilatanzwinkel ab Mψ = Mψ(ψ). Die Bedingung ψ = φ entspricht der assoziierten Fließregel; andernfalls wird die nicht-assoziierte Fließregel verwendet. Weitere Einzelheiten finden sich im theoretischen Handbuch. Da sich der Boden letztlich in einen sogenannten kritischen Zustand überführt (kein Zuwachs der volumetrischen plastischen Dehnung beim plastischen Scheren), ist es sinnvoll, die Dilatanz zu begrenzen. Dies erfordert die Einführung eines maximalen Porenvolumens emax, bei dessen Erreichen der kritische Zustand mit ψ = 0 erwartet wird. Ein anschauliches Beispiel wird hierzu dargestellt (hier). Die Auswirkungen der Wahl des Dilatanzwinkels auf die Vorhersage des Bodenverhaltens im Vergleich zum tatsächlichen Verhalten werden ebenfalls erläutert (hier).Zur Verdeutlichung ist in der folgenden Abbildung eine grafische Darstellung der Entwicklung der volumetrischen Dehnung unter Berücksichtigung einer Dilatanzbegrenzung (Dilation Cutoff) dargestellt.
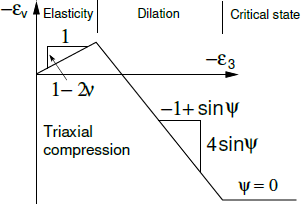 Entwicklung der volumetrischen plastischen Dehnung mit Dilatanzbegrenzung
Entwicklung der volumetrischen plastischen Dehnung mit Dilatanzbegrenzung
Die grundlegenden Materialparameter, die das Drucker-Prager-Modell definieren, sind in der folgenden Tabelle aufgeführt. Diese Parameter können sowohl bei Berechnungen unter dränierten Bedingungen als auch unter undränierten Bedingungen vom Typ (1) – d. h. Berechnung in effektiven Spannungen (cef, φef) verwendet werden. Wird hingegen Typ (2) gewählt – also die Berechnung in effektiven Spannungen auf Basis der undränierten Scherfestigkeit (Su) – so wird der Wert der effektiven Kohäsion c durch den Wert der undränierten Scherfestigkeit Su ersetzt. Der effektive Reibungswinkel φ = φu wird in diesem Fall auf null gesetzt, also φ = φu . Die Drucker-Prager-Fließfläche wird dann durch die Mises-Fließfläche ersetzt (siehe unten). Die Steifigkeitsparameter werden jedoch weiterhin als effektive Werte angenommen.Bei undränierten Bedingungen wird im Allgemeinen davon ausgegangen, dass der Boden keine Dilatanz zeigt. Daher wird für beide Varianten der Dilatanzwinkel ψ = 0 angesetzt.
Aus der Materialparameter-Tabelle wird ersichtlich, dass das Drucker-Prager-Modell – ähnlich wie das modifizierte elastische Modell – zwischen dem Bodenverhalten bei primärer Belastung und bei Ent- bzw. Wiederbelastung unterscheidet. Dies geschieht durch Einführung eines Ent-/Wiederbelastungsmoduls Eur, siehe auch das Mohr-Coulomb-Modell.
Symbol | Einheit | Beschreibung | |
| [MPa] | Elastizitätsmodul | |
| [MPa] | Ent-/Wiederbelastungsmodul | |
| [-] | Querdehnungszahl | |
| [kPa] | Effektive Kohäsion | |
| [°] | Effektiver Reibungswinkel | |
| [°] | Dilatanzwinkel | |
| [kN/m3] | Eigengewicht | |
| [-] | Anfangs-Porenzahl entsprechend dem Zustand am Ende des ersten Rechenschritts | |
| [-] | Maximale Porenzahl zur Begrenzung der Dilatanz | |
| [1/K] | Wärmedehnungskoeffizient (bei Berücksichtigung von Temperatureinflüssen) |
Bei der Wahl undränierter Bedingungen vom Typ (3) – also der Berechnung in Gesamtspannungen Su – wird die Drucker-Prager-Fließfläche erneut durch die Mises-Fließfläche ersetzt. In ähnlicher Weise wird die Mohr-Coulomb-Fließfläche durch die Tresca-Fließfläche ersetzt. Eine grafische Darstellung dieser Variante ist in der Abbildung enthalten. Diese Option berücksichtigt φ = ψ = 0, was der assoziierten Fließregel entspricht. Da hierbei ein volumenunveränderliches Material modelliert wird, wird der Wert der Querdehnungszahl ν typischerweise im Bereich von 0,49 bis 0,499 gewählt. Es ist zu beachten, dass ein zu großer Wert nahe 0,5 numerische Instabilitäten verursachen kann. Im besten Fall führt dies zu ungenauen Ergebnissen.Weitere Informationen finden Sie im theoretischen Handbuch.
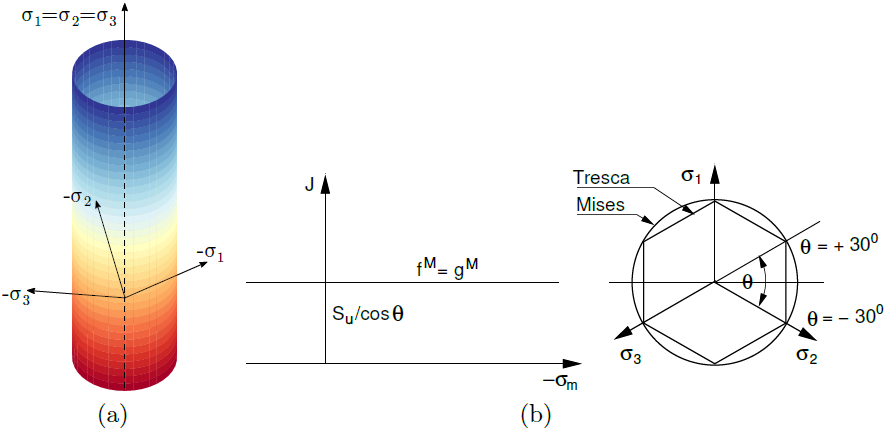 a) Fließfläche im Hauptspannungsraum, b) Projektion in die deviatorische Ebene und c) Meridionalebene
a) Fließfläche im Hauptspannungsraum, b) Projektion in die deviatorische Ebene und c) Meridionalebene
Die Materialparameter zur Definition der Mises- bzw. Tresca-Fließfläche sind in der folgenden Tabelle angegeben.Im Fall der Mises-Fließfläche ist der Wert des Lode-Winkels θ konstant und beträgt ± 30°.
Symbol | Einheit | Beschreibung | |
Eu | [Pa] | Undränierter Elastizitätsmodul | |
Su | [Pa] | Undränierte Scherfestigkeit | |
ν | [-] | Querdehnungszahl im Bereich 0,49 – 0,499 | |
γ | [kN/m3] | Eigengewicht | |
α | [1/K] | Wärmeausdehnungskoeffizient (bei Berücksichtigung von Temperatureinflüssen) |
Das Drucker-Prager-Modell erlaubt – ähnlich wie das Mohr-Coulomb-Modell – die Durchführung von Standsicherheitsberechnungen. Dabei können sowohl die klassische Böschungsstabilitätsanalyse als auch eine Stabilitätsanalyse innerhalb eines bestimmten Rechenschritts (Bauphase) durchgeführt werden.In beiden Fällen erfolgt die Berechnung durch eine schrittweise Reduktion der Scherfestigkeitsparameter c, φ wobei ein Reduktionsfaktor ζ eingeführt wird:
![]()
Dabei sind c, φ die tatsächlichen Scherfestigkeitsparameter, cd, φd die reduzierten Parameter.Der Sicherheitsbeiwert FS ergibt sich daraus wie folgt:
![]()
Ebenso wird der Dilatanzwinkel ψ reduziert, sofern ψ ≠ 0 vorgegeben ist.Die Implementierung des Drucker-Prager-Materialmodells im GEO5 FEM-Programm ist ausführlich im theoretischen Handbuch beschrieben.